Code: https://github.com/felipeOL10/Option_data_Russell2000/blob/main/Option_data_analysis.ipynb

The Black-Scholes model

The Black-Scholes model is a funtion of time, stock price, implied volatility and the interest rate.

The sensitivity of an option to the variables above is called the "Greeks".

1st order greeks:

Delta: The delta of a call option indicates how much its price changes in response to changes in the underlying asset price. It can range from 0 to 1 for a call option, and from -1 to 0 for a put option. The delta tells us how closely the option price tracks the movements of the underlying asset.

Theta: represents the time decay of an option's value. It tell us how much the option price decreases over time due to the passage of time. In theory limits for theta are not explicitly defined because they depend on multiple factors like time to expiration, volatility, and interest rates.

Rho: It indicates how much the option price changes when interest rates fluctuate. Values for rho generally range from 0 to positive infinity, and for put options, it ranges from negative infinity to 0.

Vega: Shows how much the option price changes in response to changes in the volatility of the underlying asset. The limits for vega are not explicitly defined as they depend on the pricing model and other factors. Vega is typically positive for both call and put options.

2nd order greeks

Gamma: Indicates how quickly the delta of an option adjusts to movements in the underlying asset. Gamma limits are not specifically stated, but it tends to be higher for options that are close to the current market price and decreases as options move further away from that price.

Volga: Volga, also known as vega convexity, captures the sensitivity of vega to changes in volatility. It shows how vega itself changes as volatility fluctuates. Limits for volga are not explicitly defined and depend on the pricing model and other factors.

Vanna: shows how the delta of the option changes in response to shifts in volatility. The values vanna can take are not explicitly stated and depend on the pricing model and other factors.

Analysing volatility

In the Black-Scholes model, the volatility is assumed to be constant. Therefore, by ploting the volatility of the option we should get a flat line, as well as a flat volatility surface. However, as we can see on the plots below this is not in accordance with reality.

• The smile: It describes the situation where implied volatility tends to be higher for both out-of-the-money (OTM) and in-the-money (ITM) options compared to at-the-money (ATM) options with the same expiration date. This results in a U-shaped curve when plotting implied volatility against strike price. The smile indicates that the market assigns higher probabilities to extreme price movements or "fat tails" in the underlying asset.

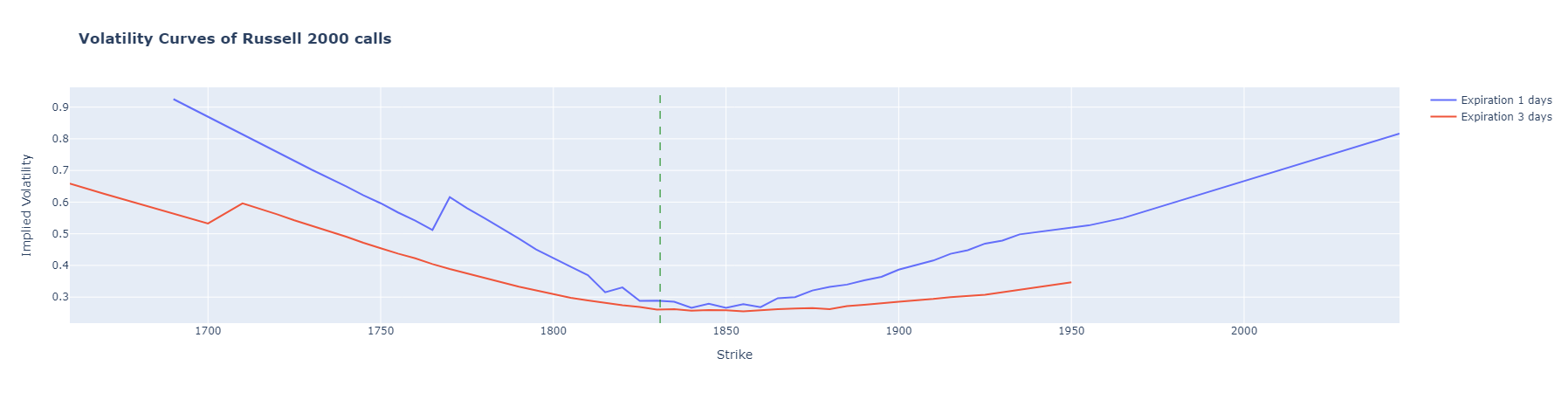The Skew: In a volatility skew, the implied volatility tends to be higher for OTM options compared to ATM options. This means that the market expects larger price movements in one direction (e.g., downside) compared to the other direction. The skew is often observed in equity markets where there may be a higher demand for protective put options, leading to increased implied volatility for OTM puts.

Analysing the greeks

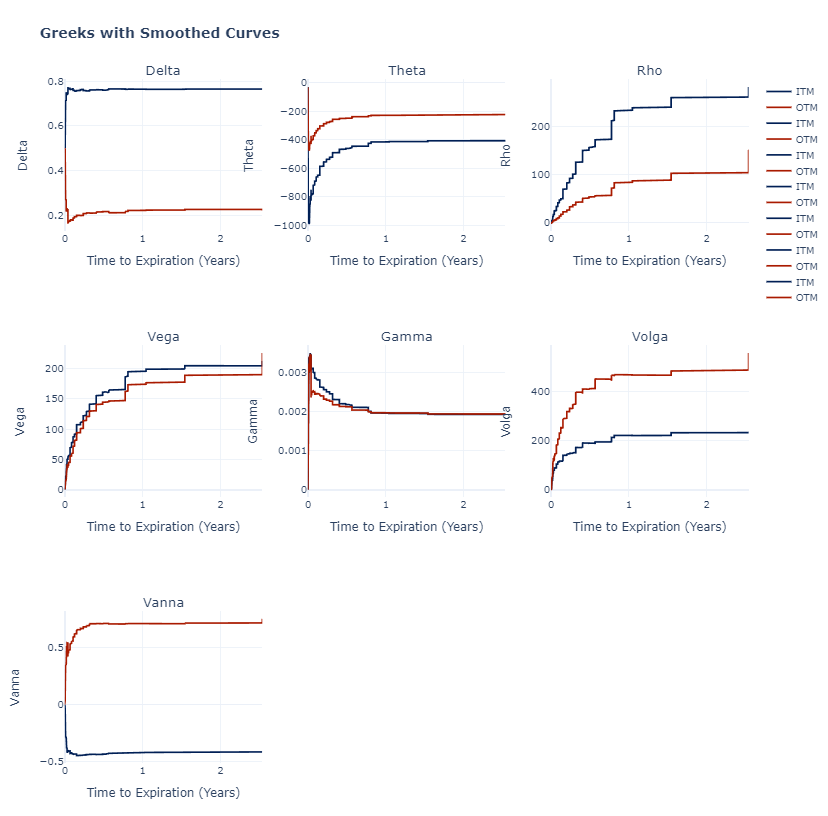
• The delta shows that ITM options have higher deltas then OTM options, in fact, this is expected because the delta can also be represented as the probability of a options expire ITM;

• The theta is negative for both ITM and OTM options, especilly for OTM options with more negative values. This is because ITM options already have intrinsic value, reducing the impact of time decay on their overall value. OTM options, on the other hand, have higher Theta values and are more affected by time decay due to their higher likelihood of expiring worthless if they remain out of the money.

• For the vega, ITM option have higher value than OTM, meaning that changes in implied volatility have a more significant impact on the value of ITM options. This is because ITM options have a higher likelihood of being exercised and, therefore, their value is more influenced by changes in volatility.

• In term of the rho, both ITM and OTM options benefit with rising interest rates.

• ITM options exhibit higher Gamma values, meaning their Delta and value change more rapidly in response to changes in the underlying asset's price. OTM options, on the other hand, have lower Gamma values and are less affected by small changes in the underlying price.

• OTM options show higher volgas than ITM, meaning their Vega and value change more rapidly in response to changes in implied volatility.

• ITM options have higher Vanna values compared to OTM options. This means that as implied volatility changes, ITM options experience larger shifts in their Delta, resulting in a more significant impact on their value.

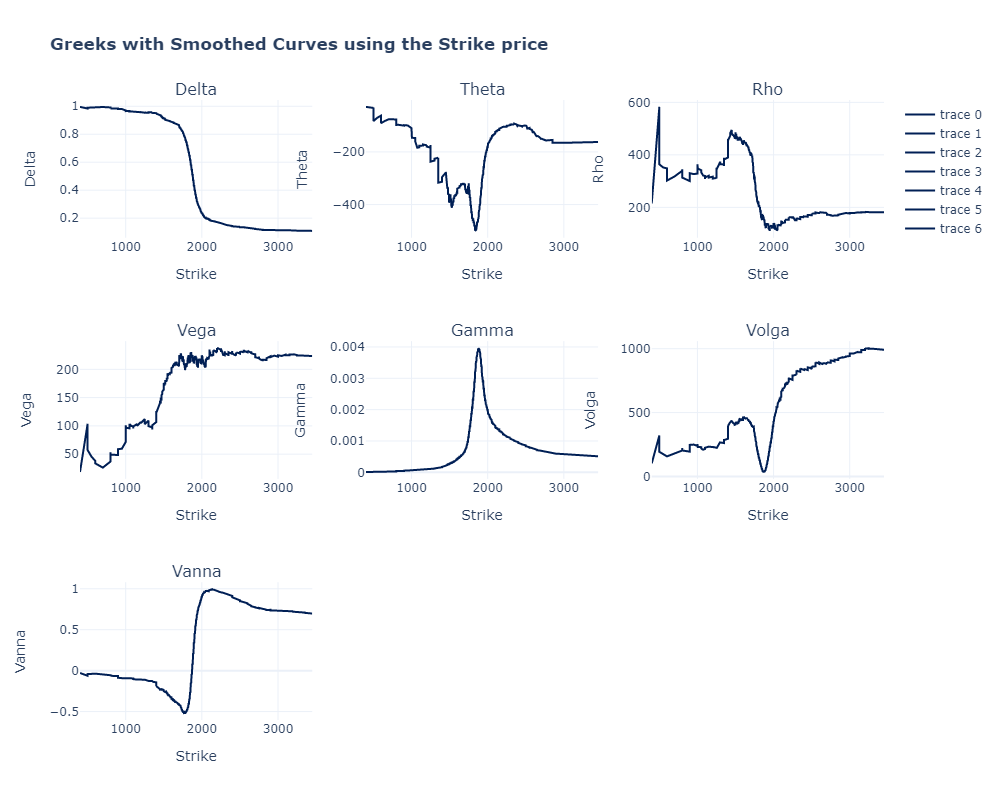
• Delta is higher for lower strike prices and lower for higher strike prices. This means that in-the-money call options have a higher sensitivity to changes in the underlying asset's price compared to out-of-the-money call options.

• Theta is higher for options with shorter time to expiration and decreases as the time to expiration increases. Therefore, options with higher strike prices (OTM) tend to have higher Theta values compared to options with lower strike prices (ITM). OTM call options are more susceptible to time decay.

• Options with lower strike prices tend to have higher Rho values compared to options with higher strike prices.

• OTM options are more sensitive to changes in implied volatility given by the evga. This could be due to higher implied volatility for OTM options, smaller intrinsic value in OTM options, higher reliance on implied volatility for OTM options' value, or market expectations of future volatility.

• Strike prices closer to the current price have higher Gamma values compared to options with strike prices further away.

• The closer to the market price the lower the sensitivity to changes in the vega. Also, OTM options show the highest values, meaning that are the most sensitive to changes in the implied volatility.

• Options with higher Vanna values near at-the-money will have larger changes in their Delta for small price movements in the underlying asset and changes in implied volatility.